Gravity shows the shape of Earth (I need your help!)

I need your help! A few posts ago, I tried to measure the shape of the Earth using my acceleration chips in my macbook. After a quick sensitivity analyses I found out that the precision of the chips was not sufficient to do this exercise. However, I really want to see if I can measure the curvature of the Earth by looking at its gravity field. So instead of high-tech measurements with my macbook, I want to see if a low-tech solution (a string pendulum) is more accurate.

The basic physics behind a pendulum measurement. The relationship between the period (T) of the pendulum and its length (l) and the local gravity (g) is (yes, high school again):

Well, this is not entirely correct, but for this experiment (keep the amplitude low!!!) it is good enough (take a look here to get a better relationship). So, to measure the local gravity (g) we need to know the length of the pendulum (half-measure!!!) and the period of the pendulum.

So, what is my set-up? A piece of string with a weight of some sort attached to the end, such that it can move freely. Also I have a half-measure to measure the length of the string. For the experts out there, a temperature and air pressure measure instrument, which could be handy to determine the drag of the pendulum.

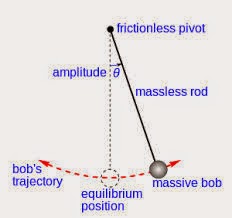Schematic of the pendulum experiment obtained from Wikipedia

As we all learned in high school, the amount of mass does not influence the period of a pendulum. However, it does influence the amount of loss due to drag (ballistic coefficient, see my blogpost), so use a weight with substantial mass. I use a mass around 5 kg. Finally, some sort of stopwatch or clock!

Oh, and know at which latitude you do the experiment (as accurate as possible). Find the latitude on a map, GPS device or use Google Earth. We want to see the relation between gravity and latitude!

Lets start the experiment!

1. Measure the length of the pendulum (rotation point to center of mass of the weight). Do this every measurement, because this could change due to temperature differences. This measurement must be done with a precision of 4 digits. So for a string of 1 meter, the absolute length must be know within a mm.
2. (This one is for the experts!) Look at the temperature and pressure instruments. Write them down.
3. Let your pendulum swing! Don't start with a too large angle (losses are strongest), but also not to small (difficult to measure period accurately). Lets say, 5-10 degrees.
4. Start the stopwatch when the pendulum has no velocity, so at one of its highest points. This is much easier to time exactly, then when the pendulum is moving very fast (in the middle of the swing). Let the pendulum swing 50 times (or 10, however this will not give enough precision in your time measurement) and divide the measure period by 50 (or 10). This reduces the timing error and makes the measurement more precise.
5. Calculate the measured gravity and repeat this experiment several times (calculate the mean and standard deviation).

My results are listed below:

Latitude: N 51 deg 59' 04.2'' ±0.2''

Height: 7 ±5m

Measurement 1: 9.8155 m/s^2

Measurement 2: 9.8012 m/s^2

Measurement 3: 9.8212 m/s^2

Measurement 4: 9.8126 m/s^2

Measurement 5: 9.8254 m/s^2

Measurement 6: 9.8083 m/s^2

Final gravity measurement: 9.814 ± 0.0087 m/s^2 (one standard deviation)

Now It is up to you! Can you do the same and send me your measurements? Lets see if we can get a global coverage (at all latitude) and try to measure the shape of the Earth!

Good luck!