Observing gravity on a moving ship
In the beginning of the 20th century the gravity field of the Earth was only measured on land. Of course, to obtain a complete image of the Earth's gravity field the oceanic area (covering 74% of the Earth) should also be inspected. However, in those days that was a difficult task. Gravity could be measured by several different instruments, but for them to work a stable platform was needed. This is difficult to arrange on a rocking ship. For example, the falling mass principle was used by Simon Stevin (1548-1620), who dropped balls of lead from the New Church in Delft, Netherlands. Later, a dutch sailor and scientist called Christiaan Huygens (1629-1695) found the relation between the period of a pendulum and gravity (I used this relation earlier in the my blog).
This is now called the Christiaan's Huygens law. With it the operator was able to measure gravity with a single pendulum, but needed a stable platform, such that horizontal movement did not interfere with the motion of the pendulum. There were already some attempts to solve this problem (e.g. the Stückrath apparatus), but it was Vening Meinesz, who in 1923 designed, built and tested his instrument, showing that it was possible to observe the gravity field on the oceans of the Earth with great accuracy.
During my lectures about professor Vening Meinesz and his work, I often get the question how his instrument worked. So, I will try to explain its basic principles in this blogpost. If you want to know the exact working I have to redirect you to the professor's publication "Theory and Practise of Pendulum Observations at Sea", Vening Meinesz (1929), but beware its is heavy-reading.
Lets start with the basics of a pendulum in motion. And to keep it simple, I am talking about the spherical-chickens-in-vacuum-kind of pendulum. What I mean is that I neglect air resistance, elongation differences because of temperature changes, slowing down due to friction in the rotation point, finite stiffness of the beam, and other small effects that deviate the stable motion of a pendulum. Below you can see my spherical-chickens-in-vacuum pendulum in motion:
 |
| Motion of a free pendulum (don't get hypnotised) |
I have released this particular pendulum from a starting angle of 20 degree. Due to the gravity pull on the mass (the bob), the pendulum starts to swing back and forth between 20 and -20 degrees. The motion of the pendulum can be described by a simple linearised differential equation. The derivation of this relation (in several ways) can be found here.
The angle of the pendulum is depicted by theta, gravity is given by g, and the length of the pendulum is l. I have created the figure above with this relation, a propagator (see this blog post), and some MATLAB coding. So, back to the gravity! When you know the length of the pendulum and measure its period you are able to determine the gravity that the pendulum is experiencing. And NO! This is not the same everywhere on the globe, I already explained this here. A problem arises when the pendulum is not fixed to a stable platform, like a moving vessel on the ocean. I tried to illustrate this by enforcing a harmonic horizontal acceleration to the free moving pendulum (see red bar).
 |
| Motion of a forced pendulum. The red bar indicates the strength and direction of the horizontal acceleration. |
You can see that the motion of the pendulum is disturbed and a single unambiguous period is difficult to determine. This is where Vening Meinesz apparatus comes into play. He used two similar pendulums with equal length, swinging in the same plane (well actually three, but lets stick to the basics).
 |
| Two pendulum swinging in the same plane. Vening Meinesz measured the distance between the two pendulums. |
He let the two pendulums swing in opposite manner and measured the difference of the two angles (or the distance between the two bobs does the same trick) and determined its period. The same thing can be done with pendulum that are experience a horizontal forcing, like the rocking of the boat. The beauty of this subtraction of the motion of both pendulums is that the horizontal forcing is cancelled. This can be seen in the following illustration:
 |
| Two pendulum swinging in the same plane and experiencing horizontal forcing |
Both pendulums experience irregular motion due to the horizontal forcing (e.g. swinging of the vessel), however the distance between the two bobs is regular. This a little bit difficult to see, so I have plotted the horizontal motion and distance over time:
 |
| The horizontal motion of the two pendulums and their distance over time |
The irregular motion of the individual bobs is clearly visible, but the horizontal distance (or the difference in their angles) is regular. The period of this distance is similar to the period of the pendulums if they stood in a stable environment. This remarkable piece of mathematics and physics enabled professor Vening Meinesz (and a submarine) to measure the gravity field of the Earth on the oceans. It kick-started the dutch and global marine research in the solid earth. Up until 1956, Vening Meinesz' apparatus was the only way to measure the gravity field on the oceans with great accuracy.
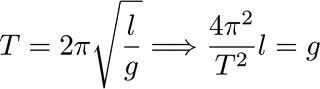




Reacties
Een reactie posten